In the wake of traditional rationalists versus empiricists debates, innateness and learning issues will never get old. In the field of numerical cognition, this takes the form of arguments regarding an allegedly innate, evolutionarily conserved and phylogenetically widespread “number sense” (Dehaene, 1999; Nieder, 2017), which is thought to underlie numerosity discriminations in both humans and other animals (Nieder, 2018). While this hypothesis has gained considerable popularity over the years, it continues to be animatedly debated.
Surprisingly, however, what is disputed is not if something about numerical discriminations is innate, but precisely what constitutes this natural mechanism. The evolutionary advantages of discriminating quantities are evident for many animal species and in numerous ecological niches (Rugani, 2018), but this does not directly endow animals with mathematical proficiency. What is the difference between discriminating quantities and working with arithmetic, counting, numbering? Can studying the brain clarify these issues?
In the light of recent evidence, hypotheses regarding an innate number system in the brain will be critically evaluated, with particular attention to avoid the loose terminology sometimes used in the field (Núñez, 2017). By showing what is innate and what depends on enculturation, better assistance can be provided to individuals who struggle to reach full mathematical proficiency, reducing the impact that low numeracy has both on individual life achievements (Parsons & Bynner, 2005) and nations’ economies (Butterworth et al., 2015).
Evidence for the innate number sense
The notion of an innate number system in the brain, first systematised by Dehaene (1999), has gained supporting evidence from various fields.
Firstly, there is evidence coming from prelinguistic infants (Cordes & Brannon, 2008), which shows that they can discriminate between small numerosities (1-4) of item sets in habituation (Strauss & Curtis, 1981) or violation of expectation paradigms (Kobayashi et al., 2005).
Secondly, studies on both trained and naive animals, from insects (Dacke & Srinivasan, 2008) to fish (Agrillo & Bisazza, 2018), birds (Rugani, 2018), and mammals (McComb et al., 1994) show that the ability to discriminate between quantities and small numerosities is not only prelinguistic but also phylogenetically widespread and advantageous in diverse ecological contexts.
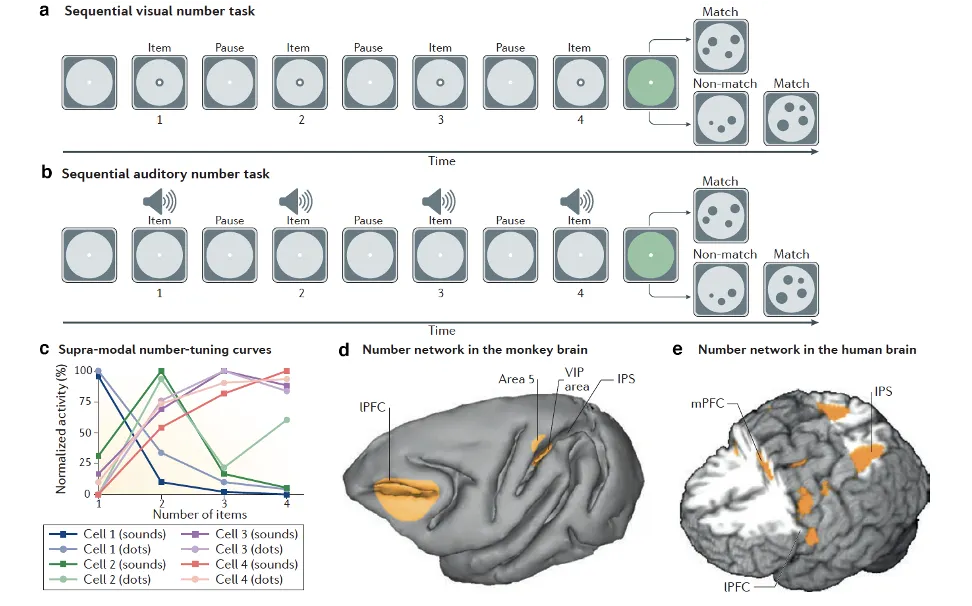
Thirdly, electrophysiological work on monkeys trained to discriminate quantities revealed the presence of numerosity-selective neurons in prefrontal (Nieder et al., 2002) and parietal areas (Nieder & Miller, 2004; Figure 1d). These neurons have since been demonstrated to be active in a wide variety of tasks and across sensory modalities (Nieder, 2012; Figure 1a, 1b). Interestingly, numerosity-selective neurons show a gaussian-like activation profile across quantities, higher for their preferred numerosity and gradually lower for neighbouring ones (Figure 1c). This type of population response in overlapping tuning curves is thought to underlie the observation that numerosity judgments are subject to the psychophysical Weber-Fechner law, determining the well-established size, distance, and ratio effects (Dehaene, 2003).
Lastly, studies on adult humans also seem to support a “number sense”. In particular, functional MRI studies show consistent activation in the prefrontal cortex (PFC) and intraparietal sulcus (IPS) during numerosity discriminations (Figure 1e), areas homologous to regions in the primate brain where “number neurons” have been found (Nieder & Dehaene, 2009). Additionally, psychophysics evidence indicates that numerosity is a stimulus characteristic subject to adaptation (Burr et al., 2018), which is taken as evidence of a dedicated perceptual mechanism.
What is innate?
It is immediately important to note that the evidence just surveyed can be un-controversially used to argue only for the innateness of an approximate quantity discriminating mechanism, which only rarely (i.e., for numerosities less than five) and often upon training results in exact quantification (Núñez, 2017). Elsewhere called an Approximate Number System (ANS; Feigenson et al., 2004), here this terminology is explicitly avoided because it implicitly uses the concept of number as a pre-existing primitive – existing where? – to which inexact mental representations are approximated (Núñez, 2017). In fact, though in the field the terms number, numerosity, and quantity are often used interchangeably, the notion of number more precisely entitles exact symbolic quantifiability, abstractness and cardinality, all properties that far from being innate and elementary depend on human cultural elaborations (Núñez, 2017).
Accordingly, additional proposals using loose terminology regarding the innateness of more elaborate mechanisms beyond quantity discrimination will also be omitted from discussion (examples are the Mental Number Line, Dehaene, 1999, and Spatial Numerical Associations more broadly, Dehaene et al., 1993), for such mechanisms are far less supported by the evidence and object of extensive criticism (Núñez et al., 2011; Shaki & Fischer, 2018).
Again, the only point to which various strains of evidence and perspectives converge is a phylogenetically widespread neural system for approximate quantities’ representation and estimation.
Interestingly, small numerosities (up to four objects) are more accurately estimated than larger ones, a feature traditionally used to argue for the presence of two qualitatively different systems in representing quantities (Burr et al., 2018; Feigenson et al., 2004). However, recent modelling evidence shows that this behaviour can clearly arise from a single system processing numerosities optimally under the resource constraint of visual memory capacity (Cheyette & Piantadosi, 2020). This also clarifies why infants and other animals (with the possible exception of chimpanzees; Tomonaga & Matsuzawa, 2002) have a lower subitising range and are usually worse in numerosity discriminations than human adults.
Furthermore, it has been shown how numerosity discrimination and numerosity-selective units can emerge in deep neural networks designed for visuospatial processing (Zorzi & Testolin, 2018), reframing the innateness of the “number sense” in terms of cognitive architectural constraints during perceptual learning. This way, numerosity is seen as a “statistical invariant in highly variable input” (Zorzi & Testolin, 2018) that gets readily picked up by various perceptual systems, possibly justifying why quantity discriminations can be carried out even by insects.
From this brief discussion, it is clear how the innate “number sense” is perhaps best understood as a “sense of approximate numerosity” (Nieder & Dehaene, 2009), whose innateness might be best understood with reference to learning biases in early sensory processing (Zorzi & Testolin, 2018).
Magnitude
So far in this evaluation, as for a long time in the numerical cognition field (Leibovich et al., 2017), it has been taken for granted that the “number sense” is capable of extracting and computing numerosity exclusively, independently of continuous magnitudes, i.e., all other physical properties of a stimulus (size, area, density, duration) that highly correlate with numerosity.
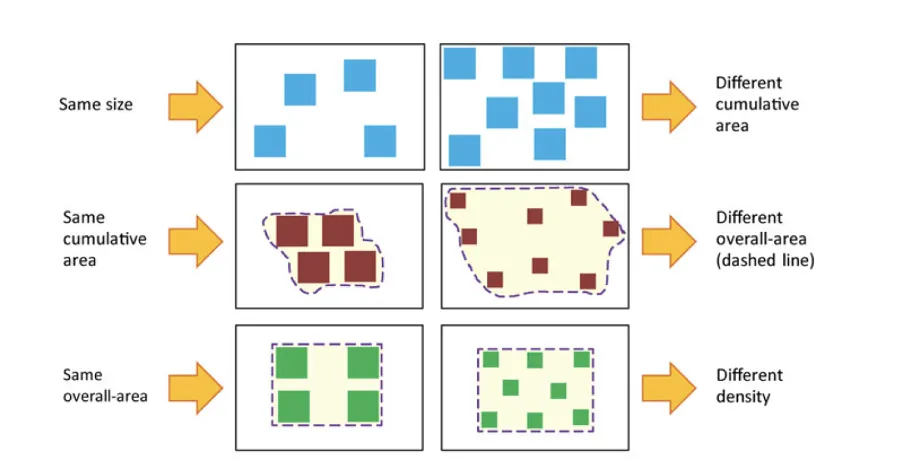
Notably, even if researchers studying numerosity comparisons often employ different control methods to try to break the correlation between numerosity and continuous magnitudes, it has been argued that this is practically impossible (Figure 2; Leibovich et al., 2017). Consequently, the large body of studies on the “number sense” could be said to support a more basic “sense of magnitude” (Leibovich et al., 2017).
Far from being a theoretical stunt, this view is supported by various lines of evidence.
First, it has been known almost from their discovery that number neurons, especially in the IPS, are active also during judgments of continuous magnitudes such as items’ physical size and location (Fias et al., 2003; Nieder & Dehaene, 2009), and are thus not selectively responding to numerosity.
Second, electrophysiological studies show how responses related to continuous sensory properties of stimuli are difficult to disentangle from numerosity processing, which they seem to influence (Gebuis et al., 2016; Gebuis & Reynvoet, 2014; Leibovich et al., 2017).
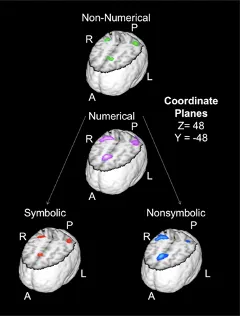
Third and finally, recent fMRI meta-analyses extend electrophysiological findings and strongly support the idea that regions across the frontal and parietal cortex support a general magnitude processing system. Specifically, in two subsequent meta-analyses on overall 150 neuroimaging studies in numerical cognition, Sokolowski and colleagues (Sokolowski, Fias, Bosah Ononye, et al., 2017; Sokolowski, Fias, Mousa, et al., 2017) compared activation responses during non-symbolic magnitude, non-symbolic numeric and symbolic numeric processing tasks. Summarised in Figure 3, their results revealed that no regions in the parietal or frontal lobes were exclusively active for numerosities that were not also active for non-numerical magnitudes. However, additional areas were recruited in processing the former.
This led them to conclude that “numbers are processed using both a generalized magnitude system and format-specific number regions” (Sokolowski, Fias, Bosah Ononye, et al., 2017).
From magnitude to numbers
How does one get from the innate magnitude system we have established to the rich tasks we usually associate with numbers in daily life?
The difference between the predisposed “sense of magnitude” and acquired numerical proficiency is manifold.
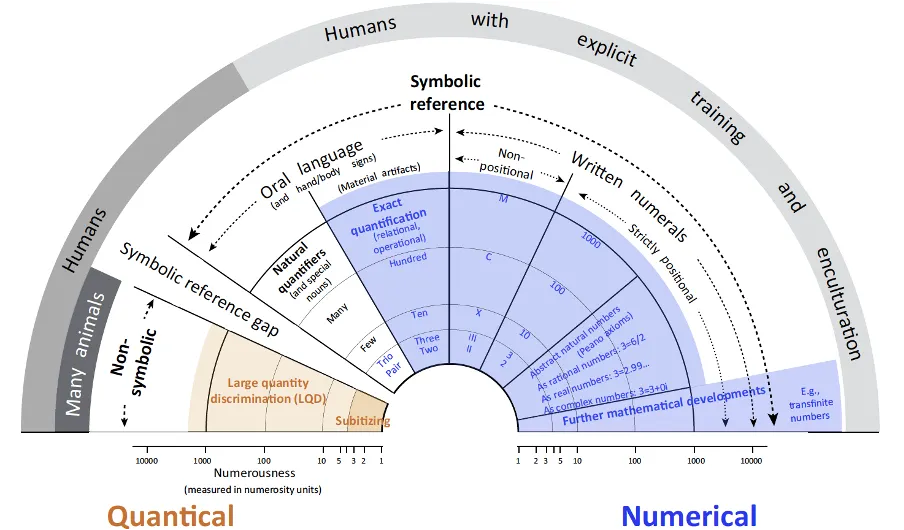
To begin with, the distinction is cultural. Or better, it depends on enculturation. For example, many isolated cultures exist with only limited numeral systems (Bowern & Zentz, 2012; Pica et al., 2004). What they often have in common is the presence of only approximate quantifiers above the subitising range and the consequent incapacity of carrying out exact arithmetic with arbitrarily large numbers. The crucial importance of this is that the capacity for number, intended as generalized precise quantification, is not innate but cultural, dependent on symbolic reference (Núñez, 2017).
Therefore, the quantical cognition (Núñez, 2017) both humans and animals are capable of is only a biologically evolved precondition for higher numerical cognition proper (Figure 4). It is not a precursor of it in a teleological sense. An evolved capacity for magnitude processing supports a culturally mediated capacity for number (Núñez, 2017).
Secondly, there are differences in the brain processing the two. Though we have already seen that magnitude processing strongly overlaps with numerical processing (Sokolowski, Fias, Bosah Ononye, et al., 2017), distinct regions are also activated for numbers and calculations that are not active when working with continuous quantities or non-symbolic magnitudes.
In particular, symbolic numerical processing recruits more the left parietal lobe (Kaufmann et al., 2011), and it has been argued that this lateralisation might reflect interactions with the language system (Nieder & Dehaene, 2009). Other areas more active for symbolic numerical processing include the right supramarginal gyrus and the inferior parietal lobule, as well as the left angular gyrus (Sokolowski, Fias, Mousa, et al., 2017). This latter area, in particular, is also known to be active during retrieval of mathematical facts (Ischebeck et al., 2006), as opposed to the parietal-frontal network, which is more active during calculation. The parietal-frontal network includes not only the bilateral IPS but also regions in the frontal cortex and anterior cingulate cortex (Skagenholt et al., 2018). Activity in this system strongly reflects the involvement of both attentional and executive processes in numerical cognition. The appreciation of these contributions from a network perspective is becoming increasingly important in the field (Skagenholt et al., 2018), also in tackling impairments such as dyscalculia.
Beyond theoretical arguments: dyscalculia interventions
In modern society, numerical cognition is crucial to various aspects of daily functioning, including economic competence (Parsons & Bynner, 2005). Low numeracy is also worse for individual achievement than mediocre reading skills and a significant cost for national economies (Butterworth et al., 2015).
For these reasons, research-driven interventions to ameliorate individual numeracy skills will consistently be necessary, especially in the case of developmental dyscalculia (DD), a disorder of mathematical competence with an estimated prevalence of 5-7% (Butterworth et al., 2015).
On the neuroanatomical side, DD is consistently associated with decreased responses in the IPS during basic numerical processing tasks (Mussolin et al., 2009), as well as decreased grey matter density area in the same region (Rykhlevskaia et al., 2009). However, abnormalities are not confined to the IPS. Abnormal structure and connectivity patterns have also been detected in frontal regions (Mussolin et al., 2009; Rykhlevskaia et al., 2009).
Correspondingly, our discussion on the foundations of numerical cognition can benefit dyscalculia interventions in two ways.
By recognising that a “sense of magnitude” likely hosted in the right inferior parietal lobule (Sokolowski, Fias, Bosah Ononye, et al., 2017) is the only innate component on which higher numerical cognition rests, interventions aimed at breaking the correlation and emphasizing the difference between readily processed continuous magnitudes and full-fledged numbers may be developed, to scaffold learning of a real sense of number (Leibovich et al., 2017).
Moreover, by considering the comorbidities that often occur with dyscalculia and the increasingly appreciated role of the broader parietal-frontal network in numerical cognition, intervention strategies that do not overlook the functions of attentional and executive processes will also be essential in the coming future (Leibovich et al., 2017).
Conclusion
In the light of the evidence reviewed, the answer to the question “are numbers innate?” is a qualified no. What is innate is a phylogenetically widespread sense of magnitude, which supports approximate quantity discriminations and is hosted in a distributed network across the frontal and parietal cortices. This system is not selective for numerosity but responds to various continuous magnitudes that correlate with it.
The capacity for number proper, intended as exact symbolic quantification, is not innate but cultural, dependent on enculturation and symbolic reference. This distinction is crucial for understanding both the foundations of numerical cognition and for developing effective interventions for mathematical learning difficulties.
The challenge for future research lies in understanding how the innate magnitude system interacts with cultural learning to give rise to the rich numerical abilities that characterize human mathematical cognition.
References
Agrillo, C., & Bisazza, A. (2018). Understanding the origin of number sense: A review of fish studies. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1740), 20160511. https://doi.org/10.1098/rstb.2016.0511
Bowern, C., & Zentz, J. (2012). Diversity in the Numeral Systems of Australian Languages. Anthropological Linguistics, 54(2), 133–160.
Burr, D. C., Anobile, G., & Arrighi, R. (2018). Psychophysical evidence for the number sense. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1740). https://doi.org/10.1098/rstb.2017.0045
Butterworth, B., Varma, S., & Laurillard, D. (2015, July 30). Dyscalculia. The Oxford Handbook of Numerical Cognition. https://doi.org/10.1093/oxfordhb/9780199642342.013.001
Cheyette, S. J., & Piantadosi, S. T. (2020). A unified account of numerosity perception. Nature Human Behaviour, 1–8. https://doi.org/10.1038/s41562-020-00946-0
Cordes, S., & Brannon, E. M. (2008). Quantitative competencies in infancy. Developmental Science, 11(6), 803–808. https://doi.org/10.1111/j.1467-7687.2008.00770.x
Dacke, M., & Srinivasan, M. V. (2008). Evidence for counting in insects. Animal Cognition, 11(4), 683–689. https://doi.org/10.1007/s10071-008-0159-y
Dehaene, S. (1999). The number sense: How the mind creates mathematics (Oxford Univ. Press pbk. ed). Oxford University Press.
Dehaene, S. (2003). The neural basis of the Weber-Fechner law: A logarithmic mental number line. Trends in Cognitive Sciences, 7(4), 145–147. https://doi.org/10.1016/s1364-6613(03)00055-x
Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122(3), 371–396. https://doi.org/10.1037/0096-3445.122.3.371
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8(7), 307–314. https://doi.org/10.1016/j.tics.2004.05.002
Fias, W., Lammertyn, J., Reynvoet, B., Dupont, P., & Orban, G. A. (2003). Parietal representation of symbolic and nonsymbolic magnitude. Journal of Cognitive Neuroscience, 15(1), 47–56. https://doi.org/10.1162/089892903321107819
Gebuis, T., Cohen Kadosh, R., & Gevers, W. (2016). Sensory-integration system rather than approximate number system underlies numerosity processing: A critical review. Acta Psychologica, 171, 17–35. https://doi.org/10.1016/j.actpsy.2016.09.003
Gebuis, T., & Reynvoet, B. (2014). The neural mechanism underlying ordinal numerosity processing. Journal of Cognitive Neuroscience, 26(5), 1013–1020. https://doi.org/10.1162/jocn_a_00541
Ischebeck, A., Zamarian, L., Siedentopf, C., Koppelstätter, F., Benke, T., Felber, S., & Delazer, M. (2006). How specifically do we learn? Imaging the learning of multiplication and subtraction. NeuroImage, 30(4), 1365–1375. https://doi.org/10.1016/j.neuroimage.2005.11.016
Kaufmann, L., Wood, G., Rubinsten, O., & Henik, A. (2011). Meta-Analyses of Developmental fMRI Studies Investigating Typical and Atypical Trajectories of Number Processing and Calculation. Developmental Neuropsychology, 36(6), 763–787. https://doi.org/10.1080/87565641.2010.549884
Kobayashi, T., Hiraki, K., & Hasegawa, T. (2005). Auditory-visual intermodal matching of small numerosities in 6-month-old infants. Developmental Science, 8(5), 409–419. https://doi.org/10.1111/j.1467-7687.2005.00429.x
Leibovich, T., Katzin, N., Harel, M., & Henik, A. (2017). From ‘sense of number’ to ‘sense of magnitude’: The role of continuous magnitudes in numerical cognition. The Behavioral and Brain Sciences, 40, e164. https://doi.org/10.1017/S0140525X16000960
McComb, K., Packer, C., & Pusey, A. (1994). Roaring and numerical assessment in contests between groups of female lions, Panthera leo. Animal Behaviour, 47(2), 379–387. https://doi.org/10.1006/anbe.1994.1052
Mussolin, C., De Volder, A., Grandin, C., Schlögel, X., Nassogne, M.-C., & Noël, M.-P. (2009). Neural Correlates of Symbolic Number Comparison in Developmental Dyscalculia. Journal of Cognitive Neuroscience, 22(5), 860–874. https://doi.org/10.1162/jocn.2009.21237
Nieder, A. (2012). Supramodal numerosity selectivity of neurons in primate prefrontal and posterior parietal cortices. Proceedings of the National Academy of Sciences, 109(29), 11860–11865. https://doi.org/10.1073/pnas.1204580109
Nieder, A. (2017). Number Faculty Is Rooted in Our Biological Heritage. Trends in Cognitive Sciences, 21(6), 403–404. https://doi.org/10.1016/j.tics.2017.03.014
Nieder, A. (2018). Evolution of cognitive and neural solutions enabling numerosity judgements: Lessons from primates and corvids. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1740), 20160514. https://doi.org/10.1098/rstb.2016.0514
Nieder, A., & Dehaene, S. (2009). Representation of number in the brain. Annual Review of Neuroscience, 32, 185–208. https://doi.org/10.1146/annurev.neuro.051508.135550
Nieder, A., Freedman, D. J., & Miller, E. K. (2002). Representation of the quantity of visual items in the primate prefrontal cortex. Science (New York, N.Y.), 297(5587), 1708–1711. https://doi.org/10.1126/science.1072493
Nieder, A., & Miller, E. K. (2004). A parieto-frontal network for visual numerical information in the monkey. Proceedings of the National Academy of Sciences, 101(19), 7457–7462. https://doi.org/10.1073/pnas.0402239101
Núñez, R., Doan, D., & Nikoulina, A. (2011). Squeezing, striking, and vocalizing: Is number representation fundamentally spatial? Cognition, 120(2), 225–235. https://doi.org/10.1016/j.cognition.2011.05.001
Núñez, R. E. (2017). Is There Really an Evolved Capacity for Number? Trends in Cognitive Sciences, 21(6), 409–424. https://doi.org/10.1016/j.tics.2017.03.005
Parsons, S., & Bynner, J. (2005). Does Numeracy Matter More.
Pica, P., Lemer, C., Izard, V., & Dehaene, S. (2004). Exact and Approximate Arithmetic in an Amazonian Indigene Group. Science, 306(5695), 499–503. https://doi.org/10.1126/science.1102085
Rugani, R. (2018). Towards numerical cognition’s origin: Insights from day-old domestic chicks. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1740), 20160509. https://doi.org/10.1098/rstb.2016.0509
Rykhlevskaia, E., Uddin, L. Q., Kondos, L., & Menon, V. (2009). Neuroanatomical Correlates of Developmental Dyscalculia: Combined Evidence from Morphometry and Tractography. Frontiers in Human Neuroscience, 3. https://doi.org/10.3389/neuro.09.051.2009
Shaki, S., & Fischer, M. H. (2018). Deconstructing spatial-numerical associations. Cognition, 175, 109–113. https://doi.org/10.1016/j.cognition.2018.02.022
Skagenholt, M., Träff, U., Västfjäll, D., & Skagerlund, K. (2018). Examining the Triple Code Model in numerical cognition: An fMRI study. PLOS ONE, 13(6), e0199247. https://doi.org/10.1371/journal.pone.0199247
Sokolowski, H. M., Fias, W., Bosah Ononye, C., & Ansari, D. (2017). Are numbers grounded in a general magnitude processing system? A functional neuroimaging meta-analysis. Neuropsychologia, 105, 50–69. https://doi.org/10.1016/j.neuropsychologia.2017.01.019
Sokolowski, H. M., Fias, W., Mousa, A., & Ansari, D. (2017). Common and distinct brain regions in both parietal and frontal cortex support symbolic and nonsymbolic number processing in humans: A functional neuroimaging meta-analysis. NeuroImage, 146, 376–394. https://doi.org/10.1016/j.neuroimage.2016.10.028
Strauss, M. S., & Curtis, L. E. (1981). Infant perception of numerosity. Child Development, 52(4), 1146–1152.
Tomonaga, M., & Matsuzawa, T. (2002). Enumeration of briefly presented items by the chimpanzee (Pan troglodytes) and humans (Homo sapiens). Animal Learning & Behavior, 30(2), 143–157. https://doi.org/10.3758/BF03192916
Zorzi, M., & Testolin, A. (2018). An emergentist perspective on the origin of number sense. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1740), 20170043. https://doi.org/10.1098/rstb.2017.0043